Neriman Tokcan
Broad Institute of MIT and Harvard
Publications
Filter by type:
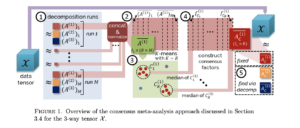
Tensor factorizations (TF) are powerful tools for the efficient representation and analysis of multidimensional data. However, classic TF methods based on maximum likelihood estimation underperform when applied to zero-inflated count data, such as single-cell RNA sequencing (scRNA-seq) data. Additionally, the stochasticity inherent in TFs results in factors that vary across repeated runs, making interpretation and reproducibility of the results challenging. In this paper, we introduce Zero Inflated Poisson Tensor Factorization (ZIPTF), a novel approach for the factorization of high-dimensional count data with excess zeros. To address the challenge of stochasticity, we introduce Consensus Zero Inflated Poisson Tensor Factorization (C-ZIPTF), which combines ZIPTF with a consensus-based meta-analysis. We evaluate our proposed ZIPTF and C-ZIPTF on synthetic zero-inflated count data and synthetic and real scRNA-seq data. ZIPTF consistently outperforms baseline matrix and tensor factorization methods in terms of reconstruction accuracy for zero-inflated data. When the probability of excess zeros is high, ZIPTF achieves up to 2.4× better accuracy. Additionally, C-ZIPTF significantly improves the consistency and accuracy of the factorization. When tested on both synthetic and real scRNA-seq data, ZIPTF and C-ZIPTF consistently recover known and biologically meaningful gene expression programs. All our data and code are available at: https://github.com/klarman-cell-observatory/scBTF and https://github.com/klarman-cell-observatory/scbtf_experiments.
A method of generating an assessment of medical condition for a patient includes obtaining a patient data tensor indicative of a plurality of tests conducted on the patient, obtaining a set of tensor factors, each tensor factor of the set of tensor factors being indicative of decomposition of training tensor data for the plurality of tests, the decomposition amplifying low-rank structure of the training tensor data, determining a patient tensor factor for the patient based on the obtained patient data tensor and the obtained set of tensor factors, applying the determined patient tensor factor to a classifier such that the determined further tensor factor establishes a feature vector for the patient, the classifier being configured to process the feature vector to generate the assessment, and providing output data indicative of the assessment.
Multimodal Tensor-Based Method for Integrative and Continuous Patient Monitoring During Postoperative Cardiac Care
Patients recovering from cardiovascular surgeries may develop life-threatening complications such as hemodynamic decompensation, making the monitoring of patients for such complications an essential component of postoperative care. However, this need has given rise to an inexorable increase in the number and modalities of data points collected, making it challenging to effectively analyze in real time. While many algorithms exist to assist in monitoring these patients, they often lack accuracy and specificity, leading to alarm fatigue among healthcare practitioners. In this study we propose a multimodal approach that incorporates salient physiological signals and EHR data to predict the onset of hemodynamic decompensation. A retrospective dataset of patients recovering from cardiac surgery was created and used to train predictive models. Advanced signal processing techniques were employed to extract complex features from physiological waveforms, while a novel tensor-based dimensionality reduction method was used to reduce the size of the feature space. These methods were evaluated for predicting the onset of decompensation at varying time intervals, ranging from a half-hour to 12 hours prior to a decompensation event. The best performing models achieved AUCs of 0.87 and 0.80 for the half-hour and 12-hour intervals respectively. These analyses evince that a multimodal approach can be used to develop clinical decision support systems that predict adverse events several hours in advance.
Deep learning and alignment of spatially-resolved whole transcriptomes of single cells in the mouse brain with Tangram
Charting a biological atlas of an organ, such as the brain, requires us to spatially-resolve whole transcriptomes of single cells, and to relate such cellular features to the histological and anatomical scales. Single-cell and single-nucleus RNA-Seq (sc/snRNA-seq) can map cells comprehensively5,6, but relating those to their histological and anatomical positions in the context of an organ’s common coordinate framework remains a major challenge and barrier to the construction of a cell atlas7–10. Conversely, Spatial Transcriptomics allows for in-situ measurements11–13 at the histological level, but at lower spatial resolution and with limited sensitivity. Targeted in situ technologies1–3 solve both issues, but are limited in gene throughput which impedes profiling of the entire transcriptome. Finally, as samples are collected for profiling, their registration to anatomical atlases often require human supervision, which is a major obstacle to build pipelines at scale. Here, we demonstrate spatial mapping of cells, histology, and anatomy in the somatomotor area and the visual area of the healthy adult mouse brain. We devise Tangram, a method that aligns snRNA-seq data to various forms of spatial data collected from the same brain region, including MERFISH1 , STARmap2, smFISH3 , and Spatial Transcriptomics4 (Visium), as well as histological images and public atlases. Tangram can map any type of sc/snRNA-seq data, including multi-modal data such as SHARE-seq data5 , which we used to reveal spatial patterns of chromatin accessibility. We equipped Tangram with a deep learning computer vision pipeline, which allows for automatic identification of anatomical annotations on histological images of mouse brain. By doing so, Tangram reconstructs a genome-wide, anatomically-integrated, spatial map of the visual and somatomotor area with ~30,000 genes at single-cell resolution, revealing spatial gene expression and chromatin accessibility patterning beyond current limitation of in-situ technologies.
Algebraic Methods for Tensor Data
We develop algebraic methods for computations with tensor data. We give 3 applications: extracting features that are invariant under the orthogonal symmetries in each of the modes, approximation of the tensor spectral norm, and amplification of low rank tensor structure. We introduce colored Brauer diagrams, which are used for algebraic computations and in analyzing their computational complexity. We present numerical experiments whose results show that the performance of the alternating least square algorithm for the low rank approximation of tensors can be improved using tensor amplification.
Newton polytopes in algebraic combinatorics
A polynomial has saturated Newton polytope (SNP) if every lattice point of the convex hull of its exponent vectors corresponds to a monomial. We compile instances of SNP in algebraic combinatorics (some with proofs, others conjecturally): skew Schur polynomials; symmetric polynomials associated to reduced words, Redfield–Pólya theory, Witt vectors, and totally nonnegative matrices; resultants; discriminants (up to quartics); Macdonald polynomials; key polynomials; Demazure atoms; Schubert polynomials; and Grothendieck polynomials, among others. Our principal construction is the Schubitope. For any subset of [?]^2, we describe it by linear inequalities. This generalized permutahedron conjecturally has positive Ehrhart polynomial. We conjecture it describes the Newton polytope of Schubert and key polynomials. We also define dominance order on permutations and study its poset-theoretic properties.
WCET Derivation Under Single Core Equivalence With Explicit Memory Budget Assignment
In the last decade there has been a steady uptrend in the popularity of embedded multi-core platforms. This represents a turning point in the theory and implementation of real-time systems. From a real-time standpoint, however, the extensive sharing of hardware resources (e.g. caches, DRAM subsystem, I/O channels) represents a major source of unpredictability. Budget-based memory regulation (throttling) has been extensively studied to enforce a strict partitioning of the DRAM subsystem’s bandwidth. The common approach to analyze a task under memory bandwidth regulation is to consider the budget of the core where the task is executing, and assume the worst-case about the remaining cores’ budgets. In this work, we propose a novel analysis strategy to derive the WCET of a task under memory bandwidth regulation that takes into account the exact distribution of memory budgets to cores. In this sense, the proposed analysis represents a generalization of approaches that consider (i) even budget distribution across cores; and (ii) uneven but unknown (except for the core under analysis) budget assignment. By exploiting the additional piece of information, we show that it is possible to derive a more accurate WCET estimation. Our evaluations highlight that the proposed technique can reduce overestimation by 30% in average, and up to 60%, compared to the state of the art.
Suppose f(x,y) is a binary form of degree d with coefficients in a field K
⊆ ℂ. The K-rank of f is the smallest number of d-th powers of linear forms over K of which f is a K-linear combination. We prove that for d≥5, there always exists a form of degree d with at least three different ranks over various fields. We also study the relationship between the relative rank and the algebraic properties of the underlying field. In particular, we show that the K-rank of a form f (such as x^3y^2) may depend on whether −1 is a sum of two squares in K. We provide lower bounds for the ℂ-rank (Waring rank) and for the ℝ-rank (real Waring rank) of binary forms depending on their factorization. We also give the rank of quartic and quintic binary forms based on their factorization over ℂ. We investigate the structure of binary forms with unique ℂ-minimal representation.
On the Waring rank of binary forms
The K-rank of a binary form f in K[x,y], K⊆ℂ, is the smallest number of d-th powers of linear forms over K of which f is a K-linear combination. We provide lower bounds for the ℂ-rank (Waring rank) and for the ℝ-rank (real Waring rank) of binary forms depending on their factorization. We completely classify binary forms of Waring rank 3.
Binary forms with three different relative ranks
Abstract
Suppose f(x,y) is a binary form of degree d with coefficients in a field K⊆ℂ. The K-rank of f is the smallest number of d-th powers of linear forms over K of which f is a K-linear combination. We prove that for d≥5, there always exists a form of degree d with at least three different ranks over various fields. The K-rank of a form f (such as x3y2) may depend on whether -1 is a sum of two squares in K.